Project description
An analysis of classical techniques for consistent stabilisation of the advection-diffusion-reaction equation finite element solution
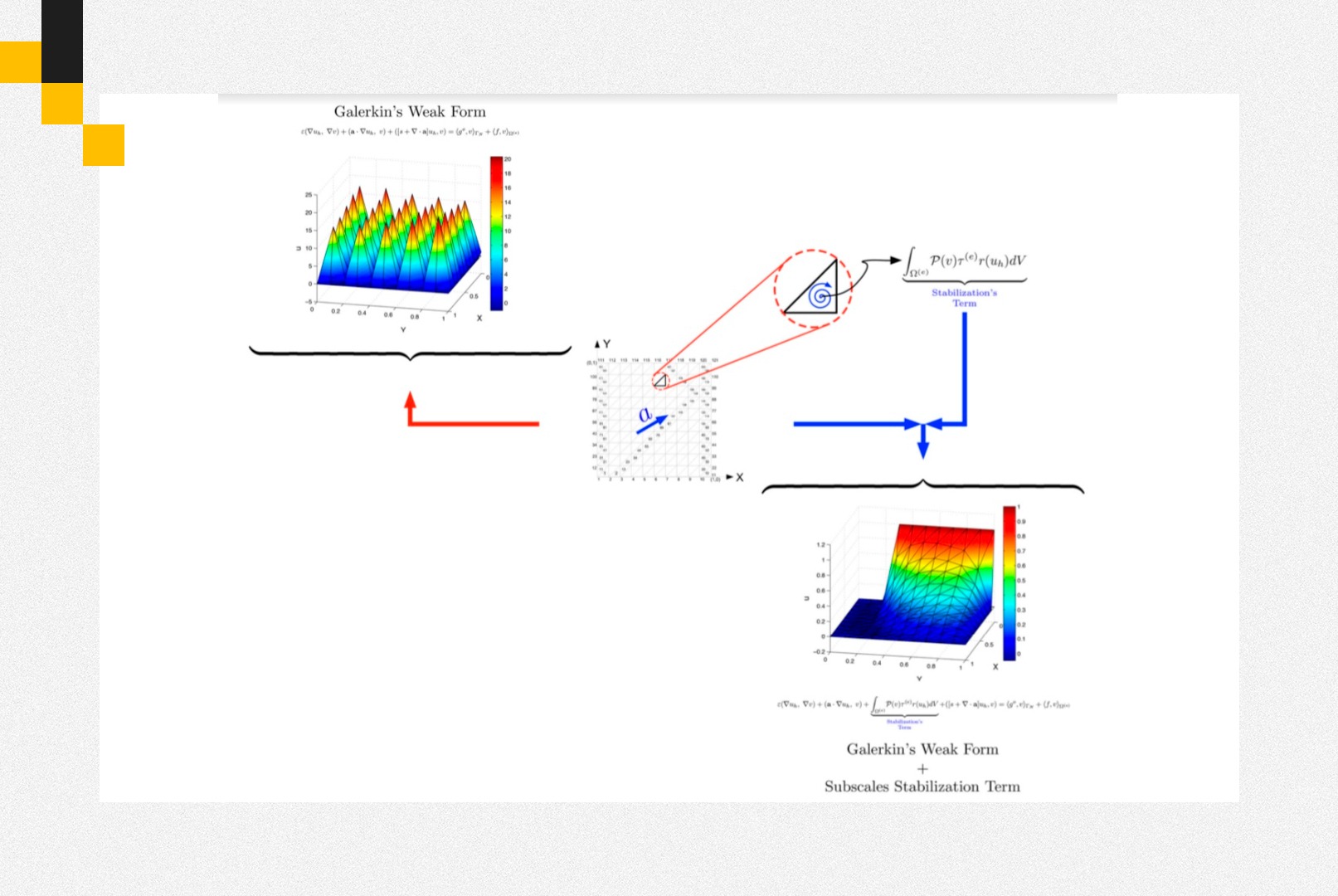
We analyse and study instability problems related to the solution of the advection–diffusion–reaction equation (ADR) using a standard finite element scheme. With this aim, this work has been carried out in the following way: first, three weak formulations are obtained from the general problem. In specific, we study the existence and uniqueness of the solution for each of the aforementioned for- mulations. Second, we analyse the general theory of consistent stabilisation techniques for the ADR equation, which includes: streamline upwind/Petrov-Galerkin (SUPG), and Galerkin/least-squares (GLS). Third, we study and develop, for linear triangular elements, two of the most important subgrid-scale techniques, i.e. algebraic subgrid scale (ASGS), and orthogonal subgrid scale (OSS). This includes the study of an expression for a stabilisation parameter based on an ADR equation’s Fourier analysis. Finally, as conclusion, all these stabilisation techniques are put in context with the SUPG technique for a better comparison as well as understanding of their underlying features for linear triangular elements.
Paper Link: https://www.tandfonline.com/doi/abs/10.1080/10618562.2020.1758315